Pascals Triangle and Combinations

Named after French Mathematician and Philosopher Blaise Pascal , the Pascals triangle is an array of binomial coefficients. 


                                                BUILDING A PASCAL TRIANGLE 


To build a Pascal Triangle , we put "1" in the beginning. Then each of the number is the sum of the two numbers above it added together, except for the corner ones, which are always equal to 1.

 

                                                            As shown in the figure , 1+3=4



                                                  PATTERNS IN A PASCAL TRIANGLE

                                                  Diagonals

As in the figure, the first diagonal of a Pascal triangle is "1", the second diagonal has the numbers in increasing order (1,2,3,4,......) . The next diagonal is the Triangular numbers, and the next one(not highlighted) is the Tetrahedral numbers 

                                                    Sums in a row 

The sum of each numbers in a row is the power of 2 of the row number (starting from 0) 

Power of 11                 

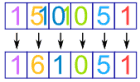
Each line is the power of 11 (This was GOD to us when we were in lower classes and were told to code for the Pascal Triangle )

and then for 11^5 , the digits just get overlapped and added

                                                              Combinations

The Pascal triangle is also used for getting combinations of any object. Suppose we have 3 balls and we want to find how many ways we can select 2 of them. So this problem takes the form "How many ways can you choose 2 objects from a set of 3 objects ? "
The answer can be found in Pascal triangle in "place 2 in row 3"(numbering starts from 0), that is 3

If we have 5 balls , how many ways can we choose 2 balls from 5 balls ? The answer is 5C2 = 10 or 2nd element in 5th row 

                                            CODE FOR PRINTING THE PASCAL TRIANGLE



The following code in C can be used to print the Pascal triangle upto any row


#include <stdio.h>   long factorial(int);   int main() { int i, n, c;   printf("Enter the number of rows you wish to see in pascal triangle\n"); scanf("%d",&n);   for ( i = 0 ; i < n ; i++ ) { for ( c = 0 ; c <= ( n - i - 2 ) ; c++ ) printf(" ");   for( c = 0 ; c <= i ; c++ ) printf("%ld ",factorial(i)/(factorial(c)*factorial(i-c)));   printf("\n"); }   return 0; }   long factorial(int n) { int c; long result = 1;   for( c = 1 ; c <= n ; c++ ) result = result*c;   return ( result ); }

More information can be found here
The pics which were used are from mathisfun.com, I am highly thankful to the site